- Joined
- Aug 30, 2002
- Messages
- 1,533
- Location
- Colorado Springs, CO USA
- Corvette
- 84 Z51 auto R.I.P. 89 black roadster SOLD
"HARMONICS"
This is one of those words that we hear alot...and used quite incorrectly...as in "harmonic balancer". Hopefully after all this it'll make sense why that term is an incorrect description of what that little round thing on the end of your crankshaft does.
From dictionary.com:
HARMONIC (as a noun):
1. Any of a series of musical tones whose frequencies are integral multiples of the frequency of a fundamental tone.
2. A tone produced on a stringed instrument by lightly touching an open or stopped vibrating string at a given fraction of its length so that both segments vibrate. Also called overtone, partial, partial tone.
3. harmonics (used with a sing. verb) The theory or study of the physical properties and characteristics of musical sound.
4. Physics. A wave whose frequency is a whole-number multiple of that of another.
Number 1 and 4 are the definitions we're going to discuss...and they basically say the same thing. 2 and 3 are a completely different meaning of "harmonics" all together...not really relevant to anything automotive. A perfect example to use in understanding harmonics is something we see all the time when looking at audio equipment, amplifiers...etc, and that is Total Harmonic Distortion (or THD), given as a percentage. I'm gonna try my best to fully explain what THD means exactly.
The first concept to go into is frequency itself. Again, from dictionary.com:
FREQUENCY:
Mathematics & Physics. The number of times a specified periodic phenomenon occurs within a specified interval
For example...if you were to pop in a CD that contained nothing but a single musical "tone" (like a recording of simply plucking a guitar string, or striking a piano key), when that tone is played back it causes the cone of the speaker to oscilliate back and forth (this is all assuming that there is no distortion in the tone!). The cone moves back and forth at some rate...or frequency. The amount of time that it takes the speaker cone to complete one single back-and-forth "cycle", that's called the "period" of oscillation. Frequency is calculated by taking the reciprocal of the period...or, Frequency = 1/T where "T" is the time to complete one cycle, or period.
This applies to lots of other motions as well...it can be a speaker cone, current flowing through a light bulb in your house, an engine vibrating on its mounts....etc. The list goes on and on.
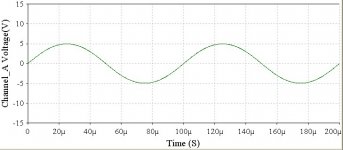
Now let's look at that motion. Ideally, if you were to plot on an X/Y graph the motion of the speaker cone, with the X axis being time and the Y axis being the position of the speaker cone...you would see a pure sine wave, and it would look something like this:

This graph is called a "time domain" plot. It shows you motion (vertical, or Y-axis) over time (horizontal, or X-axis). The name “time domain” comes from the X-axis being expressed as time. The numbers on the Y axis represent the position, or "amplitude" of the oscillation. This particular wave has a "peak-to-peak" of 10, as it "peaks" at +5 and -5. Since this particular graph has the Y-axis units as voltage, this could represent voltage being applied to the speaker coil, +5 to -5 volts (which would translate directly into cone position). A graph like this could represent 10 centimeters of speaker cone travel (ok so it's a REALLY big speaker!), or 10 thousanths of an inch of engine vibration, or 10 amps of current flowing through a light bulb (of course the units displayed in the graph would change accordingly). In this example, the sine wave has a period of 100 micro-seconds (that funky-looking little "u" means micro), which is 0.0001 seconds. So, the frequency of this wave is 1/0.0001 = 10,000 Hertz, or 10KHz (Kilo-Hertz). This is a frequency that does fall within the range of human hearing.
Just FYI: The instrument used to view the time domain plot of an electrical signal is an Oscilloscope.
Now we’re going to look at that same plot in a little different way, as a “frequency domain plot”. This type of plot is also sometimes called a “frequency spectrum plot”. Spectrum just means a range of frequencies. The difference is that the horizontal, or X-axis, is going to be expressed in frequency instead of time (which are inversely proportional from the F = 1/T equation). The vertical, or Y-axis, of a frequency domain plot is generally expressed in Decibels, which is just a logarithmic conversion from voltage, current, power…etc. Or, in some cases the Y-axis can represent those units directly…although it’s rare that method is used. We’re going to look at the definition of Total Harmonic Distortion (THD)…as you might see specified in the manual of a stereo amplifier. I think this example will give a good feel for just what a harmonic is, which is the point of all of this anyway. Power is expressed in Watts, and the conversion from Watts to Decibels is expressed as dBm, and the formula for the conversion is:
dBm = 10 * log [Power(W)/1mW]
This reads as “10 times the log of power (in Watts) divided by 1mW.
(1mW being 1 milli-Watt, or 0.001Watts)
This conversion will become important when we get to the actual calculation of THD. For now it’s only important to realize that the Y-axis of a frequency domain plot that’s expressed in Decibels is simply a logarithmic representation of the amplitude of the frequency component being displayed on the graph.
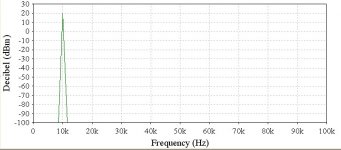
So here’s what the frequency domain plot of the same signal we looked at earlier would look like:

It’s not important to attempt to relate the Y-axis units of this plot to the Y-axis units of the first (time domain) plot. The frequency is the same, represented by the green “spike” at 10KHz. This 10KHz “frequency component” has a magnitude of 20dBm (Y-axis).
Just FYI: The instrument used to view the frequency domain plot of an electrical signal is a Spectrum Analyzer, named from the fact that it’s analyzing a spectrum, or range, of frequencies…in this case from zero Hertz to 100KHz.
At this point what is important to realize is the fact that the sine wave used in this example contains only a single frequency component (at 10KHz). We call this a “spectrally pure” sine wave.
So let’s go back to the physics definition of a “harmonic” (which DOES apply here):
A wave whose frequency is a whole-number multiple of that of another.
The “another” mentioned in this definition is what we call the “fundamental” frequency in our example.
So, based on that definition…if this wave did contain any harmonics, they would fall at the fundamental frequency multiplied by incrementing whole numbers…ie fundamental x 2 (second harmonic), fundamental x 3 (third harmonic)…so on and so on.
Harmonics are categorized as “even harmonics” and “odd harmonics”. Odd harmonics being the first, third, fifth, and so on. Even harmonics being the second, fourth, sixth, and so on. The “first harmonic” is of course equal to the fundamental frequency.
For mathematical reasons that are too intense to go into here, only “odd harmonics” are of interest to us. We’ll see why graphically in a minute.
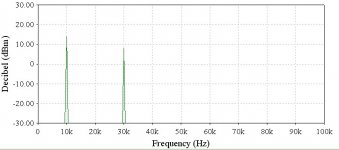
So let’s look at what happens to our nice “spectrally pure” sine wave when we add another frequency component at the third harmonic frequency. First the frequency domain plot:

Here we see the added frequency component at the third harmonic of 30KHz, which is the fundamental frequency of 10KHz x 3. Notice also that the harmonic ALWAYS has a lower magnitude than the fundamental. In this case the fundamental magnitude is about 15dBm, and the second harmonic has a magnitude of about 9dBm.
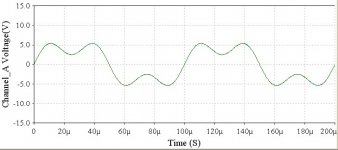
Now the really cool part…just what does that signal now look like in the time domain:

Here in the time domain plot, we can see the third harmonic frequency of 30KHz (1/30,000Hz = 33.333uS) “superimposed” on top of the fundamental frequency of 10KHz.
Interesting. So let’s add the fifth harmonic frequency component (remember, we’re only interested in ODD harmonics) and see what happens.
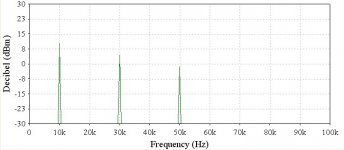
Frequency domain with third and fifth harmonic components:

Notice here that the magnitude decreases with each harmonic.
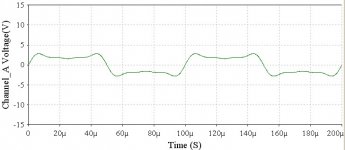
Time domain with third and fifth harmonic components:

Not so easy to distinguish the two extra frequency components here is it!
Let’s go one more, and add the seventh harmonic…
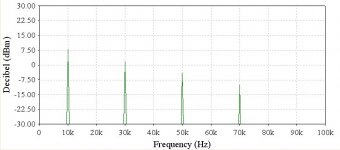
Frequency domain with third, fifth, and seventh harmonic components:

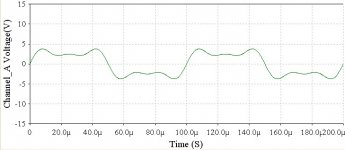
Time domain with third, fifth, and seventh harmonic components:

It is obvious by now why the frequency domain plot is so important. It shows very readily each and every frequency component contained in the now heavily distorted wave, as well as a very accurate magnitude of each single component. It is impossible to derive that information from the time domain plot. In fact, our wave is now starting to look more like a “square wave” than a sine wave. That brings up an interesting question…just what WOULD a square wave look like in the frequency domain? Let’s see!
Here’s what a square wave looks like in the time domain:

This is something like what you would see if you used an oscilloscope to probe an electrical signal in a digital system…such as the “clock” signal that drives a CPU chip. Of course this would be a VERY slow CPU at only 10KHz! We would say this signal is “on” for 50uS, and “off” for 50uS, for a total period of 100uS.
Now, here’s what that square wave would look like in the frequency domain, if you were to connect that clock signal to a spectrum analyzer:

Look at that! ONLY the odd harmonics are present! There are NO even harmonic components in a square wave (or maybe it’s more realistic to say that they are small enough to be irrelevant).
Ok so let’s move on to the definition of Total Harmonic Distortion (THD). The “text” description of THD would be “the ratio of the sum of the RMS magnitude of the harmonics to the RMS magnitude of the total power of the fundamental (desired) plus harmonics (undesired), expressed as a percentage”. Of course we have to decide just how many harmonics are to be included in the definition. For this example we will say that we’re going to consider the first two harmonic components.
FYI: RMS stands for “Root Mean Square”, and is just a statistical method for averaging a series of numbers
Mathematically, the definition goes like this:

“N” in our example would be two (based on our “text” definition of THD).
Now, the catch here is that this equation is expecting “H” to be expressed in power, or Watts…not in decibels. So, we’re gonna have to do a little math. Yuk.
So let’s look at some plots of a more realistic system and calculate the THD. These plots will represent the power levels being delivered by an audio amplifier (output), assuming a spectrally pure input sine wave.
Time domain plot of amplifier output:

Frequency domain plot of amplifier output:

So, compared to our examples above, these harmonic components are not very strong, at -50dBm and -70dBm, with the fundamental at 10dBm. Also, there is not a lot of difference in the time domain plot vs. our original time domain plot. Let’s look at the original again (which would be the amplifier input):

About the only thing that’s noticeably different is that the amplitude of the time domain plot is a wee bit lower at the output of the amplifier compared to the input. However, when we look at the frequency domain plot of the amplifier output, the two extra harmonic components are readily visible.
Allrightey then…let’s calculate the THD of this amplifier shall we?
Referring back to the equation for converting Watts to dBm:
dBm = 10 x log [Power / 1mW] (again, 1mW being 0.001W).
With a little algebraic manipulation to solve for power, we get:
Power = [10 ^ (dBm/10)] * 0.001
(read as “10 to the power of dBm divided by 10, times 0.001)
So we take each frequency component in the frequency domain plot of the amplifier output and use this equation to determine the power level of each component.
The fundamental at 10KHz is sitting at 10dBm, which yields a power level of 0.01W.
The third harmonic component at 30KHz is sitting at -50dBm, which yields a power level of 0.00000001W. (pretty small!)
The fifth harmonic component at 50KHz is sitting at -70dBm, which yields a power level of 0.0000000001W
That’s a lot of zeros! It might be a little easier on the eyes to display these power levels in micro-watts, or uW. The fundamental would be 10,000uW, the third harmonic 0.01uW, and the fifth harmonic 0.0001uW.
So now we can apply the equation for THD:

Note that H1 is the “first harmonic”, which is equal to the fundamental.
So, H1 = 10,000uW, H2 = 0.01uW, and H3 = 0.0001uW.
Plug those into the %THD equation and you get 0.001% Total Harmonic Distortion. (THAT is a good amplifier!!)
Clear as mud ain’t it!! LOL
I know this is probably horrible overkill…but the real point here is to get somewhat of an understanding if just exactly WHAT a harmonic is. So, when that little round thing on the front of our engines is referred to as a “harmonic balancer”…you’ll understand just how inaccurate that description really is. The correct term for that magical little device is a Torsion Vibration Damper (“torsion” coming from the little rubber ring separating the two halves of the thing). We don’t want our engines vibrating at ANY frequency! The job of that little gizmo is to “dampen” the FUNDAMENTAL frequency…NOT just the harmonics!
Bill
This is one of those words that we hear alot...and used quite incorrectly...as in "harmonic balancer". Hopefully after all this it'll make sense why that term is an incorrect description of what that little round thing on the end of your crankshaft does.
From dictionary.com:
HARMONIC (as a noun):
1. Any of a series of musical tones whose frequencies are integral multiples of the frequency of a fundamental tone.
2. A tone produced on a stringed instrument by lightly touching an open or stopped vibrating string at a given fraction of its length so that both segments vibrate. Also called overtone, partial, partial tone.
3. harmonics (used with a sing. verb) The theory or study of the physical properties and characteristics of musical sound.
4. Physics. A wave whose frequency is a whole-number multiple of that of another.
Number 1 and 4 are the definitions we're going to discuss...and they basically say the same thing. 2 and 3 are a completely different meaning of "harmonics" all together...not really relevant to anything automotive. A perfect example to use in understanding harmonics is something we see all the time when looking at audio equipment, amplifiers...etc, and that is Total Harmonic Distortion (or THD), given as a percentage. I'm gonna try my best to fully explain what THD means exactly.
The first concept to go into is frequency itself. Again, from dictionary.com:
FREQUENCY:
Mathematics & Physics. The number of times a specified periodic phenomenon occurs within a specified interval
For example...if you were to pop in a CD that contained nothing but a single musical "tone" (like a recording of simply plucking a guitar string, or striking a piano key), when that tone is played back it causes the cone of the speaker to oscilliate back and forth (this is all assuming that there is no distortion in the tone!). The cone moves back and forth at some rate...or frequency. The amount of time that it takes the speaker cone to complete one single back-and-forth "cycle", that's called the "period" of oscillation. Frequency is calculated by taking the reciprocal of the period...or, Frequency = 1/T where "T" is the time to complete one cycle, or period.
This applies to lots of other motions as well...it can be a speaker cone, current flowing through a light bulb in your house, an engine vibrating on its mounts....etc. The list goes on and on.
Now let's look at that motion. Ideally, if you were to plot on an X/Y graph the motion of the speaker cone, with the X axis being time and the Y axis being the position of the speaker cone...you would see a pure sine wave, and it would look something like this:

This graph is called a "time domain" plot. It shows you motion (vertical, or Y-axis) over time (horizontal, or X-axis). The name “time domain” comes from the X-axis being expressed as time. The numbers on the Y axis represent the position, or "amplitude" of the oscillation. This particular wave has a "peak-to-peak" of 10, as it "peaks" at +5 and -5. Since this particular graph has the Y-axis units as voltage, this could represent voltage being applied to the speaker coil, +5 to -5 volts (which would translate directly into cone position). A graph like this could represent 10 centimeters of speaker cone travel (ok so it's a REALLY big speaker!), or 10 thousanths of an inch of engine vibration, or 10 amps of current flowing through a light bulb (of course the units displayed in the graph would change accordingly). In this example, the sine wave has a period of 100 micro-seconds (that funky-looking little "u" means micro), which is 0.0001 seconds. So, the frequency of this wave is 1/0.0001 = 10,000 Hertz, or 10KHz (Kilo-Hertz). This is a frequency that does fall within the range of human hearing.
Just FYI: The instrument used to view the time domain plot of an electrical signal is an Oscilloscope.
Now we’re going to look at that same plot in a little different way, as a “frequency domain plot”. This type of plot is also sometimes called a “frequency spectrum plot”. Spectrum just means a range of frequencies. The difference is that the horizontal, or X-axis, is going to be expressed in frequency instead of time (which are inversely proportional from the F = 1/T equation). The vertical, or Y-axis, of a frequency domain plot is generally expressed in Decibels, which is just a logarithmic conversion from voltage, current, power…etc. Or, in some cases the Y-axis can represent those units directly…although it’s rare that method is used. We’re going to look at the definition of Total Harmonic Distortion (THD)…as you might see specified in the manual of a stereo amplifier. I think this example will give a good feel for just what a harmonic is, which is the point of all of this anyway. Power is expressed in Watts, and the conversion from Watts to Decibels is expressed as dBm, and the formula for the conversion is:
dBm = 10 * log [Power(W)/1mW]
This reads as “10 times the log of power (in Watts) divided by 1mW.
(1mW being 1 milli-Watt, or 0.001Watts)
This conversion will become important when we get to the actual calculation of THD. For now it’s only important to realize that the Y-axis of a frequency domain plot that’s expressed in Decibels is simply a logarithmic representation of the amplitude of the frequency component being displayed on the graph.
So here’s what the frequency domain plot of the same signal we looked at earlier would look like:

It’s not important to attempt to relate the Y-axis units of this plot to the Y-axis units of the first (time domain) plot. The frequency is the same, represented by the green “spike” at 10KHz. This 10KHz “frequency component” has a magnitude of 20dBm (Y-axis).
Just FYI: The instrument used to view the frequency domain plot of an electrical signal is a Spectrum Analyzer, named from the fact that it’s analyzing a spectrum, or range, of frequencies…in this case from zero Hertz to 100KHz.
At this point what is important to realize is the fact that the sine wave used in this example contains only a single frequency component (at 10KHz). We call this a “spectrally pure” sine wave.
So let’s go back to the physics definition of a “harmonic” (which DOES apply here):
A wave whose frequency is a whole-number multiple of that of another.
The “another” mentioned in this definition is what we call the “fundamental” frequency in our example.
So, based on that definition…if this wave did contain any harmonics, they would fall at the fundamental frequency multiplied by incrementing whole numbers…ie fundamental x 2 (second harmonic), fundamental x 3 (third harmonic)…so on and so on.
Harmonics are categorized as “even harmonics” and “odd harmonics”. Odd harmonics being the first, third, fifth, and so on. Even harmonics being the second, fourth, sixth, and so on. The “first harmonic” is of course equal to the fundamental frequency.
For mathematical reasons that are too intense to go into here, only “odd harmonics” are of interest to us. We’ll see why graphically in a minute.
So let’s look at what happens to our nice “spectrally pure” sine wave when we add another frequency component at the third harmonic frequency. First the frequency domain plot:

Here we see the added frequency component at the third harmonic of 30KHz, which is the fundamental frequency of 10KHz x 3. Notice also that the harmonic ALWAYS has a lower magnitude than the fundamental. In this case the fundamental magnitude is about 15dBm, and the second harmonic has a magnitude of about 9dBm.
Now the really cool part…just what does that signal now look like in the time domain:

Here in the time domain plot, we can see the third harmonic frequency of 30KHz (1/30,000Hz = 33.333uS) “superimposed” on top of the fundamental frequency of 10KHz.
Interesting. So let’s add the fifth harmonic frequency component (remember, we’re only interested in ODD harmonics) and see what happens.
Frequency domain with third and fifth harmonic components:

Notice here that the magnitude decreases with each harmonic.
Time domain with third and fifth harmonic components:

Not so easy to distinguish the two extra frequency components here is it!
Let’s go one more, and add the seventh harmonic…
Frequency domain with third, fifth, and seventh harmonic components:

Time domain with third, fifth, and seventh harmonic components:

It is obvious by now why the frequency domain plot is so important. It shows very readily each and every frequency component contained in the now heavily distorted wave, as well as a very accurate magnitude of each single component. It is impossible to derive that information from the time domain plot. In fact, our wave is now starting to look more like a “square wave” than a sine wave. That brings up an interesting question…just what WOULD a square wave look like in the frequency domain? Let’s see!
Here’s what a square wave looks like in the time domain:

This is something like what you would see if you used an oscilloscope to probe an electrical signal in a digital system…such as the “clock” signal that drives a CPU chip. Of course this would be a VERY slow CPU at only 10KHz! We would say this signal is “on” for 50uS, and “off” for 50uS, for a total period of 100uS.
Now, here’s what that square wave would look like in the frequency domain, if you were to connect that clock signal to a spectrum analyzer:

Look at that! ONLY the odd harmonics are present! There are NO even harmonic components in a square wave (or maybe it’s more realistic to say that they are small enough to be irrelevant).
Ok so let’s move on to the definition of Total Harmonic Distortion (THD). The “text” description of THD would be “the ratio of the sum of the RMS magnitude of the harmonics to the RMS magnitude of the total power of the fundamental (desired) plus harmonics (undesired), expressed as a percentage”. Of course we have to decide just how many harmonics are to be included in the definition. For this example we will say that we’re going to consider the first two harmonic components.
FYI: RMS stands for “Root Mean Square”, and is just a statistical method for averaging a series of numbers
Mathematically, the definition goes like this:

“N” in our example would be two (based on our “text” definition of THD).
Now, the catch here is that this equation is expecting “H” to be expressed in power, or Watts…not in decibels. So, we’re gonna have to do a little math. Yuk.
So let’s look at some plots of a more realistic system and calculate the THD. These plots will represent the power levels being delivered by an audio amplifier (output), assuming a spectrally pure input sine wave.
Time domain plot of amplifier output:

Frequency domain plot of amplifier output:

So, compared to our examples above, these harmonic components are not very strong, at -50dBm and -70dBm, with the fundamental at 10dBm. Also, there is not a lot of difference in the time domain plot vs. our original time domain plot. Let’s look at the original again (which would be the amplifier input):

About the only thing that’s noticeably different is that the amplitude of the time domain plot is a wee bit lower at the output of the amplifier compared to the input. However, when we look at the frequency domain plot of the amplifier output, the two extra harmonic components are readily visible.
Allrightey then…let’s calculate the THD of this amplifier shall we?
Referring back to the equation for converting Watts to dBm:
dBm = 10 x log [Power / 1mW] (again, 1mW being 0.001W).
With a little algebraic manipulation to solve for power, we get:
Power = [10 ^ (dBm/10)] * 0.001
(read as “10 to the power of dBm divided by 10, times 0.001)
So we take each frequency component in the frequency domain plot of the amplifier output and use this equation to determine the power level of each component.
The fundamental at 10KHz is sitting at 10dBm, which yields a power level of 0.01W.
The third harmonic component at 30KHz is sitting at -50dBm, which yields a power level of 0.00000001W. (pretty small!)
The fifth harmonic component at 50KHz is sitting at -70dBm, which yields a power level of 0.0000000001W
That’s a lot of zeros! It might be a little easier on the eyes to display these power levels in micro-watts, or uW. The fundamental would be 10,000uW, the third harmonic 0.01uW, and the fifth harmonic 0.0001uW.
So now we can apply the equation for THD:

Note that H1 is the “first harmonic”, which is equal to the fundamental.
So, H1 = 10,000uW, H2 = 0.01uW, and H3 = 0.0001uW.
Plug those into the %THD equation and you get 0.001% Total Harmonic Distortion. (THAT is a good amplifier!!)
Clear as mud ain’t it!! LOL
I know this is probably horrible overkill…but the real point here is to get somewhat of an understanding if just exactly WHAT a harmonic is. So, when that little round thing on the front of our engines is referred to as a “harmonic balancer”…you’ll understand just how inaccurate that description really is. The correct term for that magical little device is a Torsion Vibration Damper (“torsion” coming from the little rubber ring separating the two halves of the thing). We don’t want our engines vibrating at ANY frequency! The job of that little gizmo is to “dampen” the FUNDAMENTAL frequency…NOT just the harmonics!
Bill



 (Yes you have EMF in your house lady, your microwave is beyond our 345kv lines
(Yes you have EMF in your house lady, your microwave is beyond our 345kv lines 




